import pandas as pd import numpy as np import matplotlib as mlb import matplotlib.pyplot as plt import seaborn as sns
In [3]:
stock_data = pd.read_csv(r"C:\Users\HP\Downloads\Copy of Stock_Market_Data.csv") stock_data.head()
Out[3]:
| Date | Name | Open | High | Low | Close | Volume | |
|---|---|---|---|---|---|---|---|
| 0 | 02-01-2022 | 01.Bank | 22.83 | 23.20 | 22.59 | 22.93 | 1842350.41 |
| 1 | 03-01-2022 | 01.Bank | 23.03 | 23.29 | 22.74 | 22.90 | 1664989.63 |
| 2 | 04-01-2022 | 01.Bank | 22.85 | 23.13 | 22.64 | 22.84 | 1354510.97 |
| 3 | 05-01-2022 | 01.Bank | 22.91 | 23.20 | 22.70 | 22.98 | 1564334.81 |
| 4 | 06-01-2022 | 01.Bank | 23.12 | 23.65 | 23.00 | 23.37 | 2586344.19 |
In [8]:
stock_data['Dte']=pd.to_datetime(stock_data['Date'],dayfirst=True) stock_data.dtypes
Out[8]:
Date object Name object Open float64 High float64 Low float64 Close float64 Volume float64 Dte datetime64[ns] dtype: object
In [ ]:
Part1: Data Cleaning and Exploration: # 1. Display basic summary statistics for each column
In [13]:
summary_statistics = stock_data.describe()
print("Summary Statistics:")
print(summary_statistics)
Summary Statistics:
Open High Low Close Volume \
count 49158.000000 49158.000000 49158.000000 49158.000000 4.915800e+04
mean 157.869018 159.588214 155.906364 157.351462 5.619999e+05
min 3.900000 3.900000 3.000000 3.800000 1.000000e+00
25% 19.000000 19.300000 18.700000 19.000000 5.109475e+04
50% 40.300000 41.000000 39.535000 40.100000 1.824160e+05
75% 89.400000 90.500000 87.700000 88.700000 5.401398e+05
max 6000.000000 6050.000000 5975.000000 6000.500000 6.593180e+07
std 520.191624 523.348078 517.136149 519.711667 1.276909e+06
Dte
count 49158
mean 2022-03-31 12:56:37.436836608
min 2022-01-02 00:00:00
25% 2022-02-13 00:00:00
50% 2022-03-30 00:00:00
75% 2022-05-19 00:00:00
max 2022-06-30 00:00:00
std NaN
In [ ]:
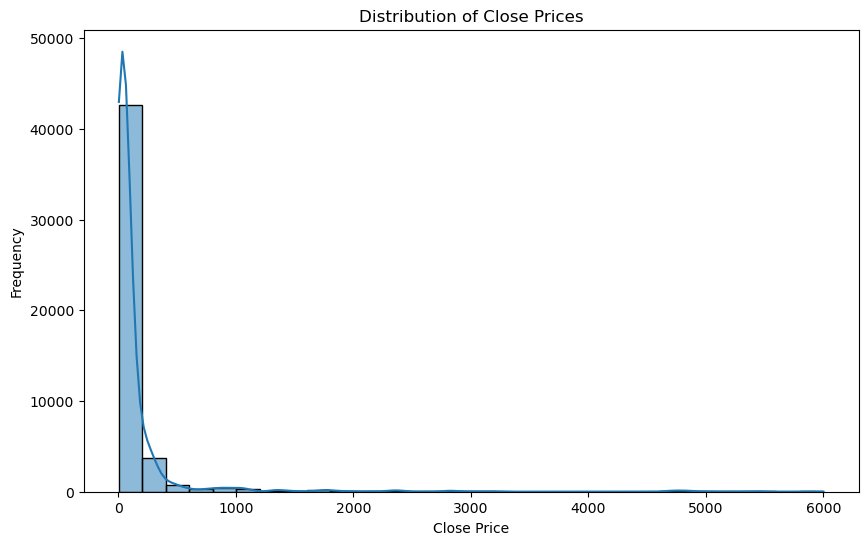
# 2. Explore the distribution of the 'Close' prices over time
In [14]:
plt.figure(figsize=(10, 6))
sns.histplot(data=stock_data, x='Close', bins=30, kde=True)
plt.title('Distribution of Close Prices')
plt.xlabel('Close Price')
plt.ylabel('Frequency')
plt.show()
C:\Users\HP\anaconda3\Lib\site-packages\seaborn\_oldcore.py:1119: FutureWarning: use_inf_as_na option is deprecated and will be removed in a future version. Convert inf values to NaN before operating instead.
with pd.option_context('mode.use_inf_as_na', True):
In [ ]:
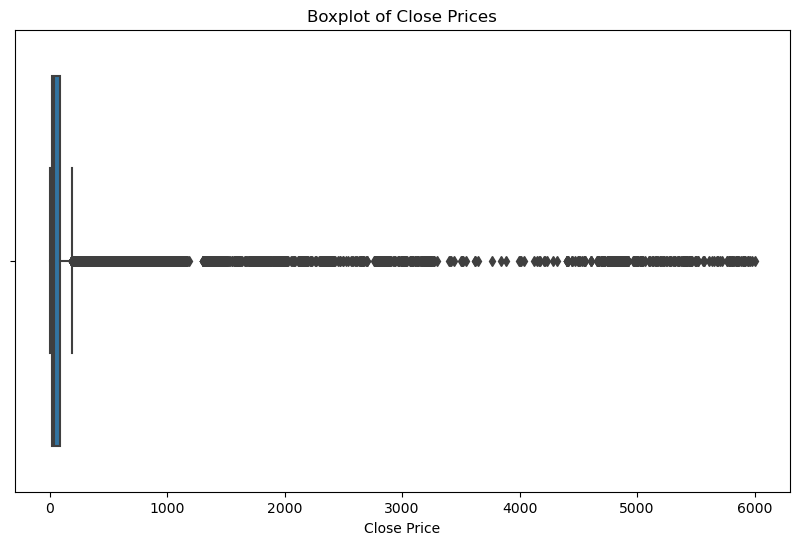
# 3. Identify and analyze any outliers in the dataset
In [15]:
plt.figure(figsize=(10, 6))
sns.boxplot(data=stock_data, x='Close')
plt.title('Boxplot of Close Prices')
plt.xlabel('Close Price')
plt.show()
In [ ]:
# Calculate outliers using IQR method
In [16]:
Q1 = stock_data['Close'].quantile(0.25)
Q3 = stock_data['Close'].quantile(0.75)
IQR = Q3 - Q1
lower_bound = Q1 - 1.5 * IQR
upper_bound = Q3 + 1.5 * IQR
outliers = stock_data[(stock_data['Close'] < lower_bound) | (stock_data['Close'] > upper_bound)]
print("Outliers:")
print(outliers)
Outliers:
Date Name Open High Low Close \
110 02-01-2022 06.Food_&_Allied 303.67 311.01 301.14 305.16
111 03-01-2022 06.Food_&_Allied 309.80 312.41 300.36 303.13
112 04-01-2022 06.Food_&_Allied 305.78 307.39 299.97 303.66
113 05-01-2022 06.Food_&_Allied 305.40 308.92 301.87 303.43
114 06-01-2022 06.Food_&_Allied 303.89 306.60 297.66 299.72
... ... ... ... ... ... ...
49043 26-06-2022 WATACHEM 204.50 211.60 204.50 207.90
49044 27-06-2022 WATACHEM 206.00 209.40 206.00 207.10
49045 28-06-2022 WATACHEM 208.90 210.10 205.00 205.80
49046 29-06-2022 WATACHEM 205.50 210.00 205.40 209.70
49047 30-06-2022 WATACHEM 210.90 215.00 207.70 214.10
Volume Dte
110 187281.15 2022-01-02
111 432190.10 2022-01-03
112 554873.95 2022-01-04
113 617348.90 2022-01-05
114 597532.50 2022-01-06
... ... ...
49043 9785.00 2022-06-26
49044 3714.00 2022-06-27
49045 13759.00 2022-06-28
49046 15023.00 2022-06-29
49047 32851.00 2022-06-30
[6960 rows x 8 columns]
In [ ]:
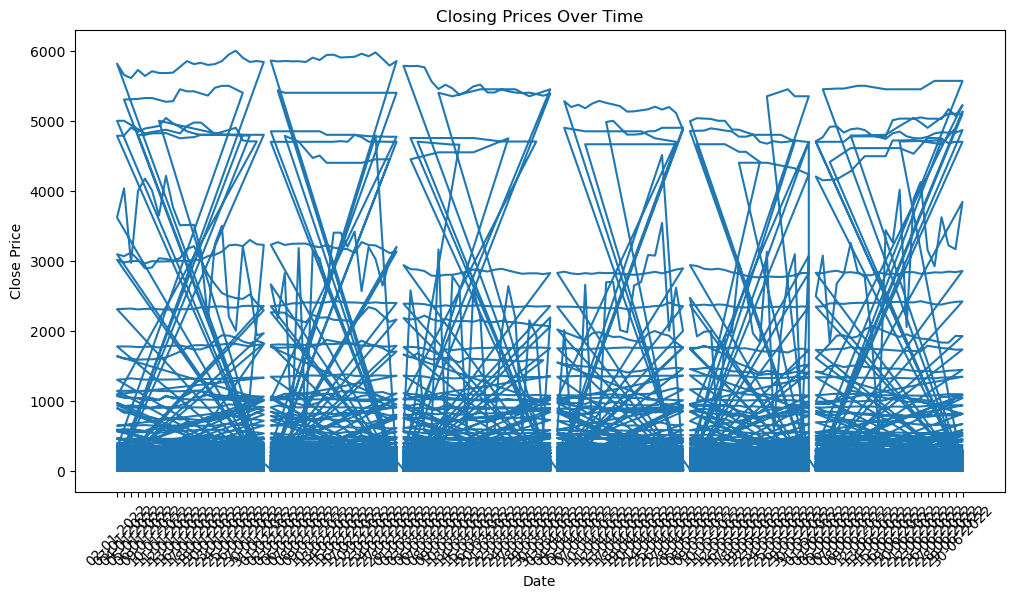
Part 2: Time Series Analysis / Rolling Window / Moving Averages: # 1. # Create a line chart to visualize the 'Close' prices over time
In [19]:
plt.figure(figsize=(12, 6))
plt.plot(stock_data['Date'], stock_data['Close'])
plt.title('Closing Prices Over Time')
plt.xlabel('Date')
plt.ylabel('Close Price')
plt.xticks(rotation=45)
plt.show()
In [ ]:
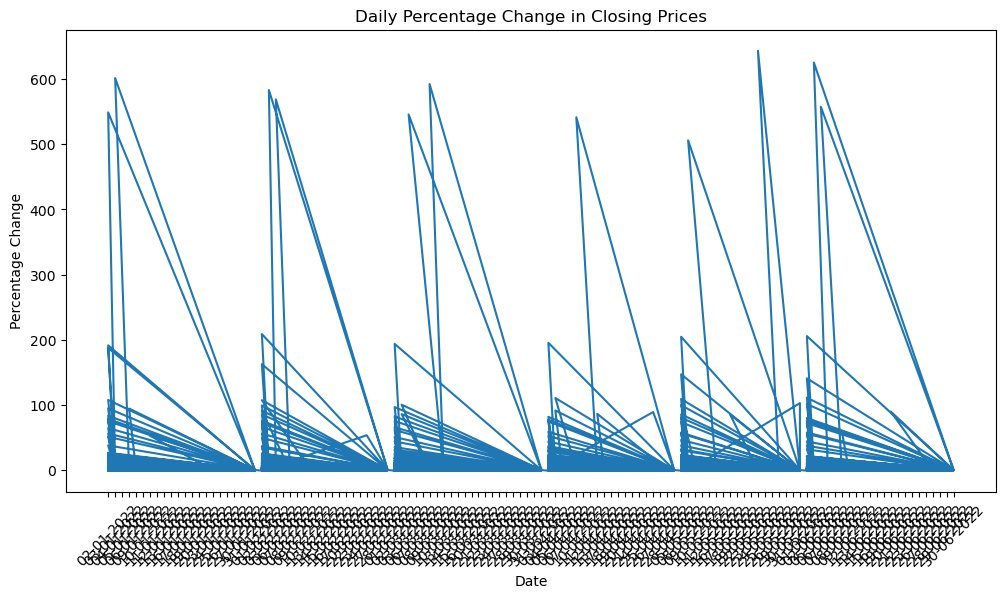
# 2. Calculate and plot the daily percentage change in closing prices
In [20]:
stock_data['Daily_Return'] = stock_data['Close'].pct_change()
plt.figure(figsize=(12, 6))
plt.plot(stock_data['Date'], stock_data['Daily_Return'])
plt.title('Daily Percentage Change in Closing Prices')
plt.xlabel('Date')
plt.ylabel('Percentage Change')
plt.xticks(rotation=45)
plt.show()
In [ ]:
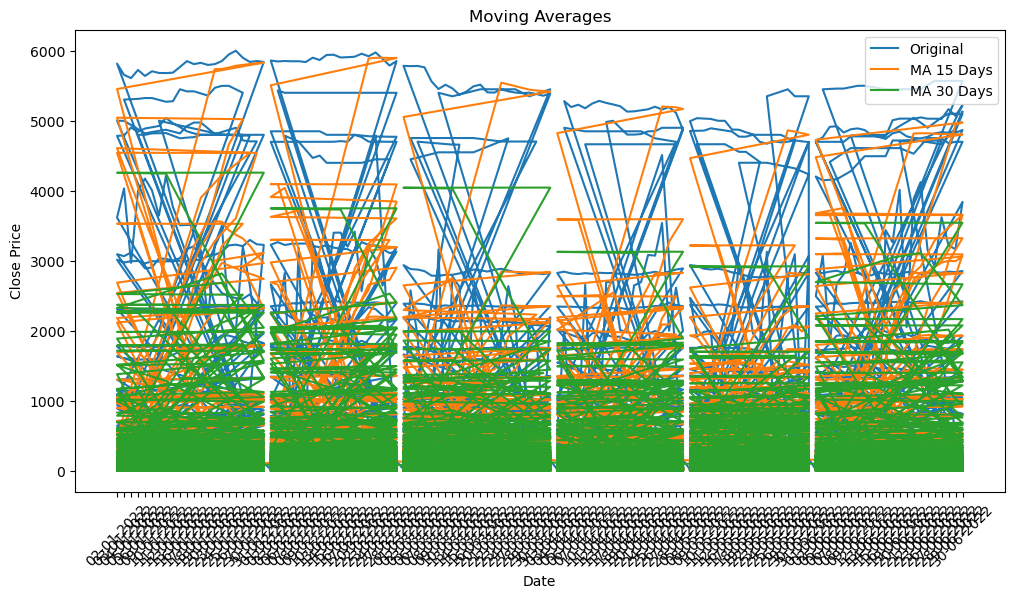
# 4. Apply moving averages to smooth the time series data in 15/30 day intervals against the original graph
In [21]:
stock_data['MA_15'] = stock_data['Close'].rolling(window=15).mean()
stock_data['MA_30'] = stock_data['Close'].rolling(window=30).mean()
plt.figure(figsize=(12, 6))
plt.plot(stock_data['Date'], stock_data['Close'], label='Original')
plt.plot(stock_data['Date'], stock_data['MA_15'], label='MA 15 Days')
plt.plot(stock_data['Date'], stock_data['MA_30'], label='MA 30 Days')
plt.title('Moving Averages')
plt.xlabel('Date')
plt.ylabel('Close Price')
plt.legend()
plt.xticks(rotation=45)
plt.show()
In [ ]:
# 5. Calculate the average closing price for each stock
In [29]:
print(stock_data.columns)
Index(['Date', 'Name', 'Open', 'High', 'Low', 'Close', 'Volume', 'Dte',
'Daily_Return', 'MA_15', 'MA_30'],
dtype='object')
In [35]:
average_closing_price = stock_data.groupby('Name')['Close'].mean()
print("Average Closing Price for Each Name:")
print(average_closing_price)
Average Closing Price for Each Name:
Name
01.Bank 21.260902
02.Cement 96.600820
03.Ceramics_Sector 71.225164
04.Engineering 132.352459
05.Financial_Institutions 29.253525
...
WMSHIPYARD 12.370492
YPL 21.339344
ZAHEENSPIN 9.964754
ZAHINTEX 7.858197
ZEALBANGLA 150.338525
Name: Close, Length: 412, dtype: float64
In [ ]:
# 6. Identify the top 5 and bottom 5 stocks based on average closing price
In [36]:
top_5_stocks = average_closing_price.nlargest(5)
bottom_5_stocks = average_closing_price.nsmallest(5)
print("Top 5 Stocks based on Average Closing Price:")
print(top_5_stocks)
print("\nBottom 5 Stocks based on Average Closing Price:")
print(bottom_5_stocks)
Top 5 Stocks based on Average Closing Price: Name APSCLBOND 5413.238636 RECKITTBEN 5342.024793 PREBPBOND 4918.357143 IBBL2PBOND 4851.330357 PBLPBOND 4836.195652 Name: Close, dtype: float64 Bottom 5 Stocks based on Average Closing Price: Name FAMILYTEX 4.698361 ICBIBANK 4.725620 FBFIF 5.289344 POPULAR1MF 5.368033 PHPMF1 5.417213 Name: Close, dtype: float64
In [ ]:
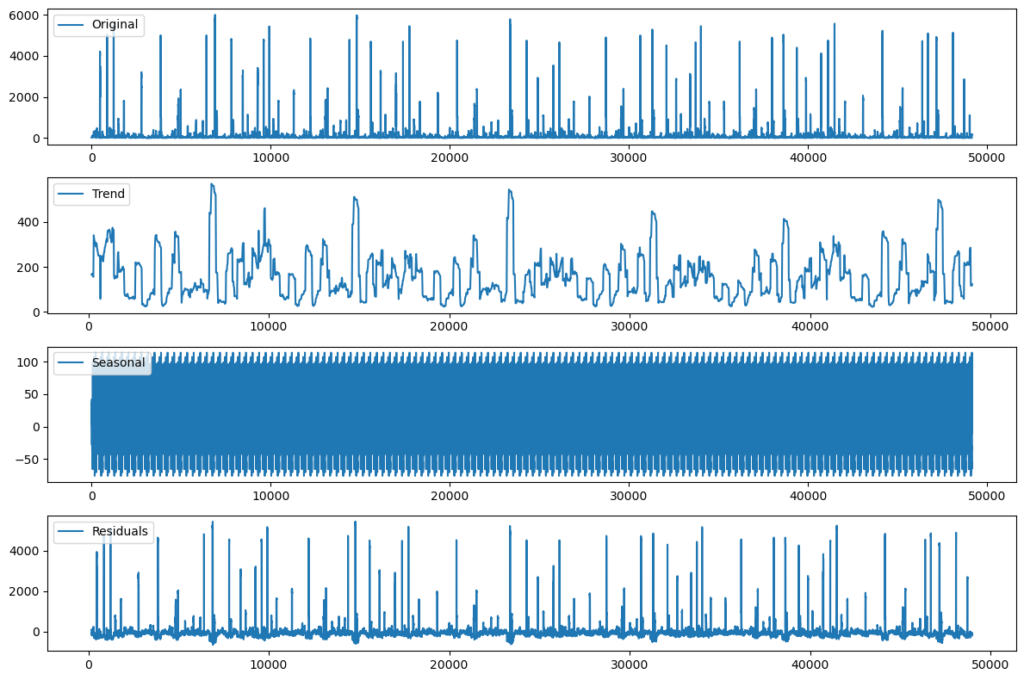
# 3. Investigate the presence of any trends or seasonality whats happen to this one
In [39]:
import statsmodels.api as sm # Perform time series decomposition result = sm.tsa.seasonal_decompose(stock_data['Close'], model='additive', period=365) # Plot the decomposition plt.figure(figsize=(12, 8)) plt.subplot(411) plt.plot(stock_data['Close'], label='Original') plt.legend(loc='upper left') plt.subplot(412) plt.plot(result.trend, label='Trend') plt.legend(loc='upper left') plt.subplot(413) plt.plot(result.seasonal, label='Seasonal') plt.legend(loc='upper left') plt.subplot(414) plt.plot(result.resid, label='Residuals') plt.legend(loc='upper left') plt.tight_layout() plt.show()
In [ ]:
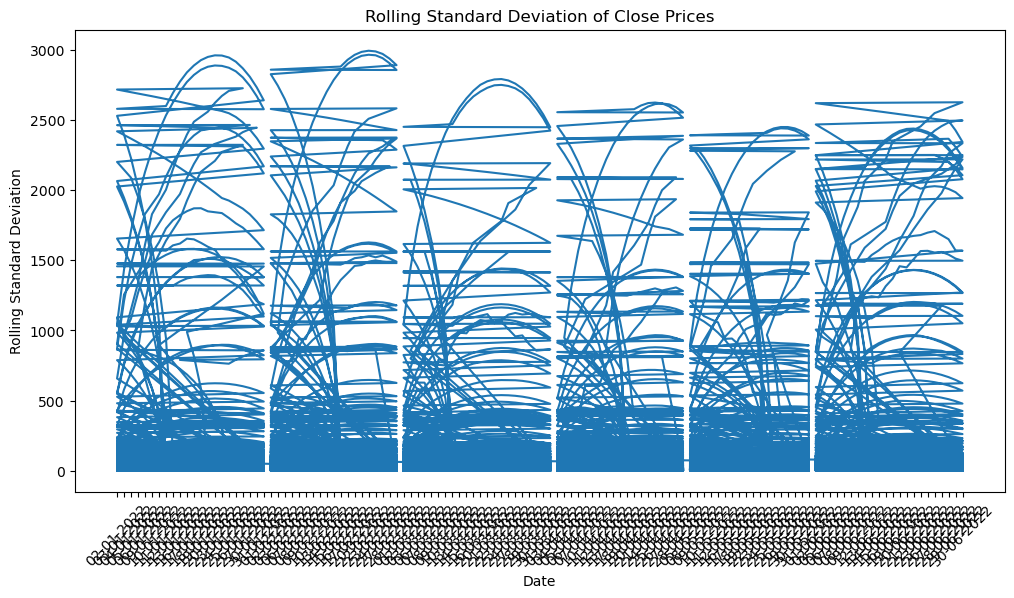
Part-3: Volatility Analysis # 1. Calculate and plot the rolling standard deviation of the 'Close' prices
In [40]:
rolling_std = stock_data['Close'].rolling(window=30).std()
plt.figure(figsize=(12, 6))
plt.plot(stock_data['Date'], rolling_std)
plt.title('Rolling Standard Deviation of Close Prices')
plt.xlabel('Date')
plt.ylabel('Rolling Standard Deviation')
plt.xticks(rotation=45)
plt.show()
In [ ]:
# 2. Create a new column for daily price change (Close - Open)
In [47]:
stock_data['Daily_Price_Change'] = stock_data['Close'] - stock_data['Open']
In [ ]:
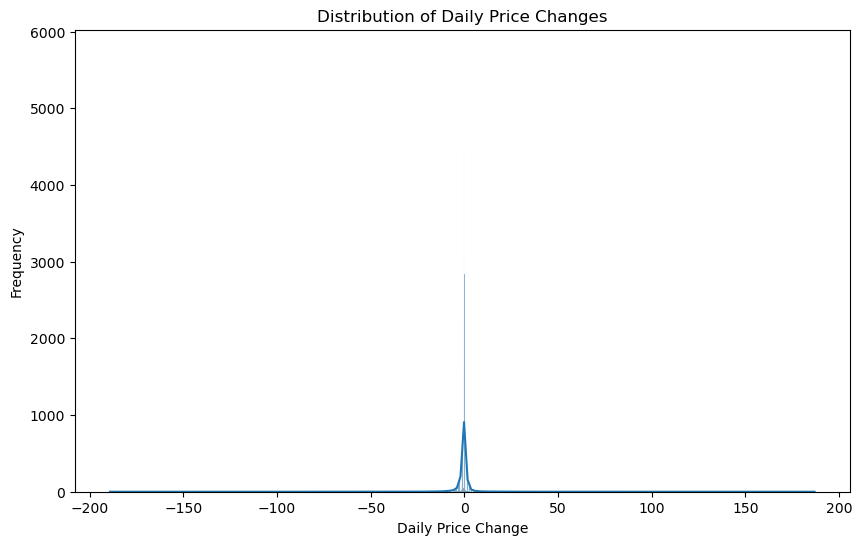
#3. Analyze the distribution of daily price changes
In [48]:
plt.figure(figsize=(10, 6))
sns.histplot(stock_data['Daily_Price_Change'], kde=True)
plt.title('Distribution of Daily Price Changes')
plt.xlabel('Daily Price Change')
plt.ylabel('Frequency')
plt.show()
C:\Users\HP\anaconda3\Lib\site-packages\seaborn\_oldcore.py:1119: FutureWarning: use_inf_as_na option is deprecated and will be removed in a future version. Convert inf values to NaN before operating instead.
with pd.option_context('mode.use_inf_as_na', True):
In [ ]:
#4. Identify days with the largest price increases and decreases
In [49]:
largest_increase = stock_data.nlargest(5, 'Daily_Price_Change')
largest_decrease = stock_data.nsmallest(5, 'Daily_Price_Change')
print("Days with Largest Price Increases:")
print(largest_increase[['Date', 'Daily_Price_Change']])
print("\nDays with Largest Price Decreases:")
print(largest_decrease[['Date', 'Daily_Price_Change']])
Days with Largest Price Increases:
Date Daily_Price_Change
48081 29-06-2022 187.0
46684 27-06-2022 145.5
46681 21-06-2022 141.5
6878 05-01-2022 125.6
44145 30-06-2022 124.5
Days with Largest Price Decreases:
Date Daily_Price_Change
23365 07-03-2022 -189.2
2774 03-01-2022 -182.5
31312 28-04-2022 -178.7
2786 20-01-2022 -166.6
6896 31-01-2022 -154.9
In [ ]:
# 5. Identify stocks with unusually high trading volume on certain days # Define unusually high volume as volume greater than 2 standard deviations from the mean
In [50]:
mean_volume = stock_data['Volume'].mean()
std_volume = stock_data['Volume'].std()
unusual_volume = stock_data[stock_data['Volume'] > (mean_volume + 2 * std_volume)]
print("\nStocks with Unusually High Trading Volume:")
print(unusual_volume[['Date', 'Name', 'Volume']])
Stocks with Unusually High Trading Volume:
Date Name Volume
52 12-01-2022 03.Ceramics_Sector 3148906.60
54 16-01-2022 03.Ceramics_Sector 3351889.00
319 17-01-2022 15.Services_&_Real_Estate 6056375.75
320 18-01-2022 15.Services_&_Real_Estate 5141492.75
321 19-01-2022 15.Services_&_Real_Estate 3928104.25
... ... ... ...
49075 08-06-2022 YPL 4296959.00
49081 16-06-2022 YPL 3394619.00
49089 28-06-2022 YPL 6145142.00
49090 29-06-2022 YPL 4463125.00
49091 30-06-2022 YPL 3844363.00
[1610 rows x 3 columns]
In [ ]:
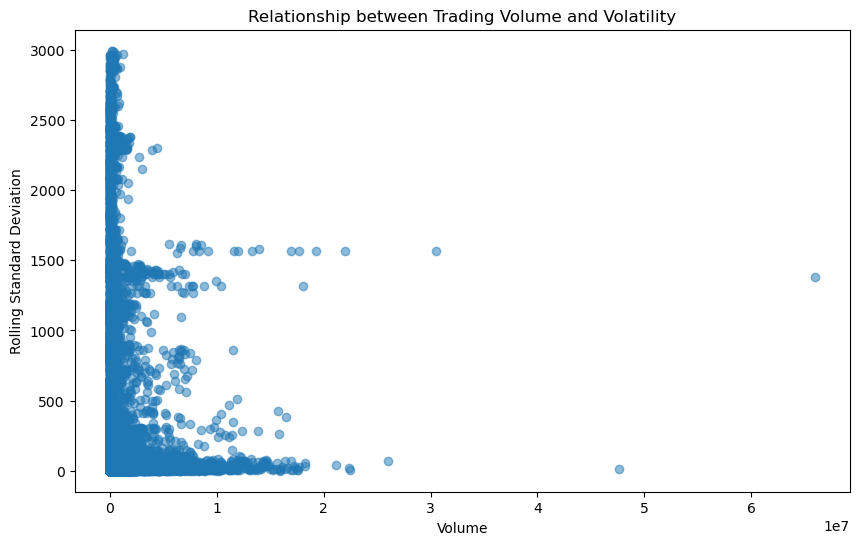
Part 4: Correlation and Heatmaps: #1. Explore the relationship between trading volume and volatility
In [51]:
plt.figure(figsize=(10, 6))
plt.scatter(stock_data['Volume'], rolling_std, alpha=0.5)
plt.title('Relationship between Trading Volume and Volatility')
plt.xlabel('Volume')
plt.ylabel('Rolling Standard Deviation')
plt.show()